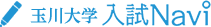第242回
三角形のフェルマー・トリチェリ点

どの角も１２０度未満の平面三角形内の点で、そこから三頂点と結ぶ線分を引くと１２０度ずつに分かれる点をフェルマー・トリチェリ点といいます（「平面三角形」の上の図と中の図の破線の交点Ｚ０）。
このときその点は、三角形内の点の中で三頂点までの距離の和を最小にします。

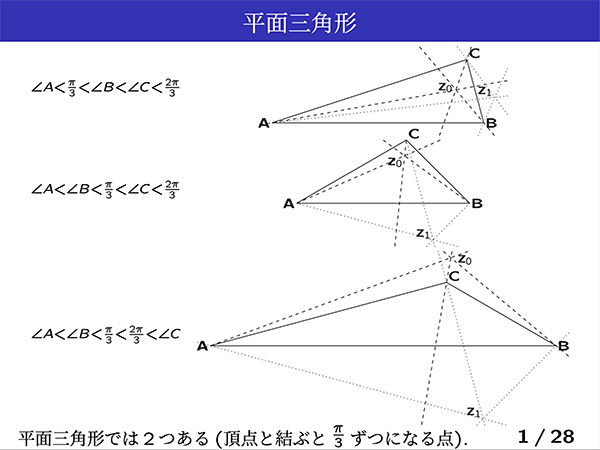
第２２６回「三角形の重心」と同様に、同じことを球面三角形（または第７回「牽引線の回転面」で述べた、球面と逆に曲がっている曲面）で考えます。すると面白いことに、１２０度ずつに分かれる点を内部に複数持つような三角形が存在することがわかります（「球面の場合」の右の図で２点、左の図ではなんと４点）。
このような場合、三頂点までの距離の和を最小にする点は、それらの点のどれかかまたは頂点のどれかになります。

以上は私の最新の論文の内容です。
このように平面三角形だけを見ていては思いもつかないようなことが起こるのが、曲面上の三角形の幾何学を考える魅力の一つです。